Linear regression in the wild

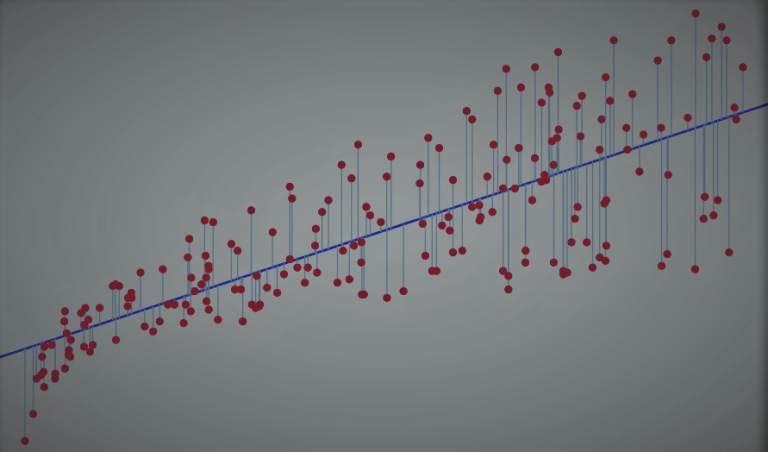
We got a consistent estimator of the parameters required for calculating $y$ given $x$ (where both have measurement errors), or in other words, the line’s coefficients.

Up until now all I’ve done is plain old linear regression. The interesting thing about this task is that $x$ has measurement error (which is typical in real world use cases).

If we want to estimate the parameters required for calculating $y$ given the exact $x$ value (without measurement error), we need to use a different approach. Using simple linear regression without accounting for $x$ being random with noise results in line slope slightly smaller than the true line slope (the line describing $x$ without measurement errors). You can read this wiki page for learning why.

I’ll use Deming regression, which is a method that can be used when the errors for the two variables $x$ and $y$ are assumed to be independent and normally distributed, and the ratio of their variances, denoted $\delta$, is known. This approach is a perfect fit for our settings, where we have

The technique used for measuring $x$ is twice as better than that for measuring $y$ in the sense of standard deviation.

So in our settings, $\delta$ is 2 squared.

Using the formulas found in the wiki page, we get